MappingOrthoMesh Class Reference

#include <mappingorthomesh.h>

Collaboration diagram for MappingOrthoMesh:

[legend]

List of all members.

Public Member Functions
void	reinit (const OrthoMesh &mesh)
void	reinit (OrthoMesh::Cell_It &cell)
virtual double	J (Point3D &p)
virtual void	Inv_T_Grad (const VecDouble &xi, Matrix &InvTGrad)
virtual void	T_grad (const VecDouble &xi, Matrix &gradT)
virtual void	T (const VecDouble &p, VecDouble &resp)
Protected Attributes
Point3D	_X0
double	_j
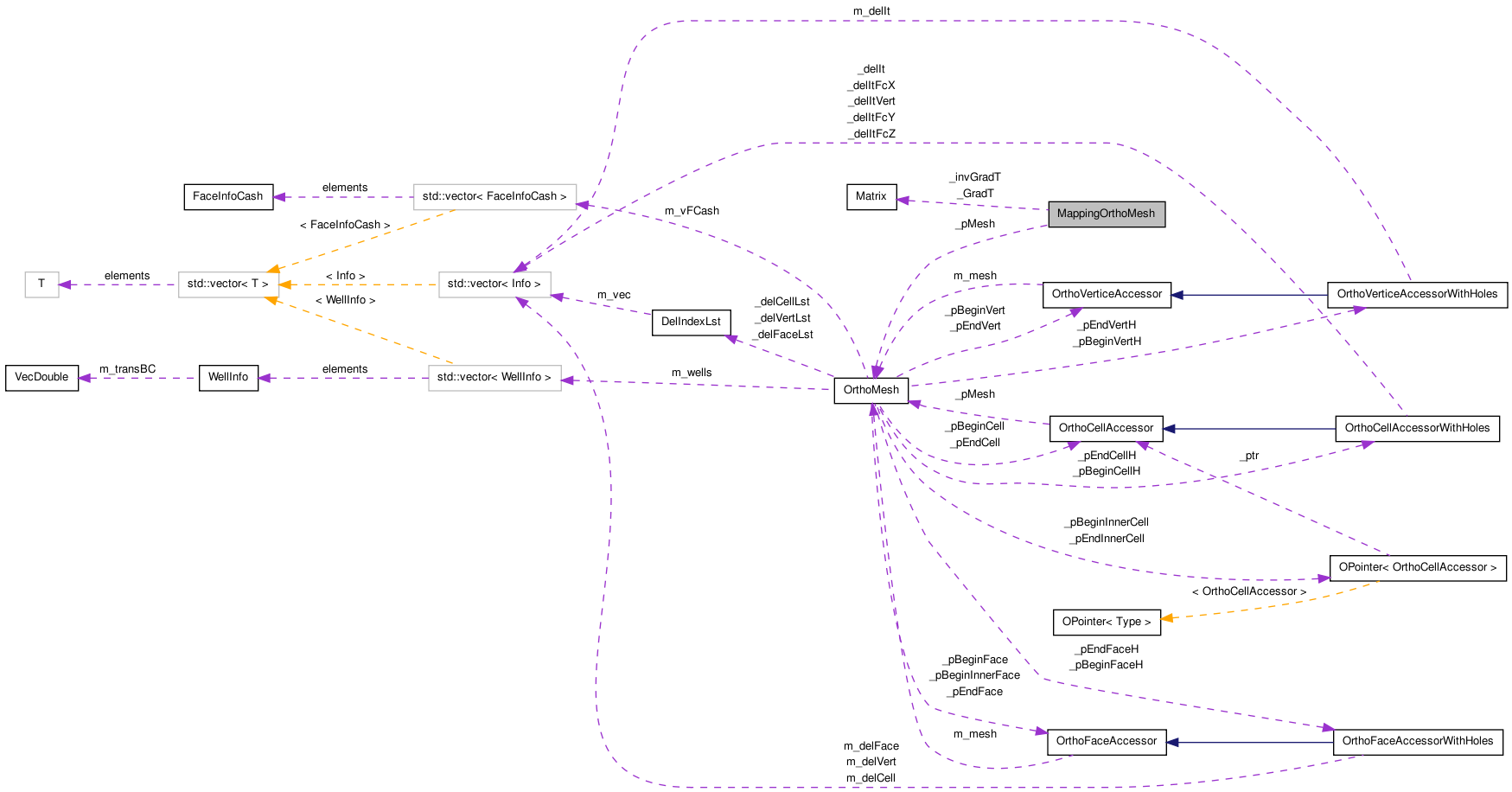
Matrix	_invGradT
Matrix	_GradT
double	_dx
double	_dy
double	_dz
const OrthoMesh *	_pMesh

---

Detailed Description

Class that defines the mapping between the unit cube and the cells of the OrthoMesh

Definition at line 12 of file mappingorthomesh.h.

---

Member Function Documentation

virtual void MappingOrthoMesh::Inv_T_Grad	(	const VecDouble &	xi,
		Matrix &	InvTGrad
	)			[inline, virtual]

Returns The derivative of the inverse of the transformation T evaluated in a point of the deformed domain x=T(xi), where xi is in reference domain.

Lets be smart here and use math to work for us. If T is a function xi -> x and InvT x->xi is its inverse then Dx InvT = 1/(Dxi T) where Dx denotes derivation in x and Dxi denotes derivation in xi.

In other words, for 1D, just returns the inverse of the value returned by the method J(xi).

This is another example of a very important truth in Computer Science: The more you know about a problem, The better you know how to solve it.

Definition at line 88 of file mappingorthomesh.h.

  {
    assert(xi.size() ==3);
    InvTGrad = _invGradT;
  }

virtual double MappingOrthoMesh::J

(

Point3D &

p

)

[inline, virtual]

Implement the Jacobian of the transformation T() where T is the function that maps points in the reference element into the deformed element. In 1D the Jacobian is just the derivative of T() evaluated in xi.

Parameters: xi = The point in the reference element Pre: x in [0:1]

Definition at line 67 of file mappingorthomesh.h.

  {
    return _j;
  }

void MappingOrthoMesh::reinit

(

OrthoMesh::Cell_It &

cell

)

[inline]

Definition at line 47 of file mappingorthomesh.h.

  {
    //Assert that the cell has as mesh,
    //the mesh passed in the reinit(OrthoMesh&) method
    assert(&(cell->getMesh()) == _pMesh); 
    cell->vertex(VERTEX_000,_X0);
  }

void MappingOrthoMesh::reinit

(

const OrthoMesh &

mesh

)

[inline]

Definition at line 23 of file mappingorthomesh.h.

  {
    _j=mesh.cellVolume();
    _invGradT.reinit(3,3);
    _GradT.reinit(3,3);
    _invGradT=0.0;
    _GradT=0.0;

    _dx=mesh.get_dx();
    _dy=mesh.get_dy();
    _dz=mesh.get_dz();
    
    _invGradT(0,0)=1.0/_dx;
    _invGradT(1,1)=1.0/_dy;
    _invGradT(2,2)=1.0/_dz;

    _GradT(0,0)=_dx;
    _GradT(1,1)=_dy;
    _GradT(2,2)=_dz;
    _pMesh = &mesh;
  }

virtual void MappingOrthoMesh::T	(	const VecDouble &	p,
		VecDouble &	resp
	)			[inline, virtual]

The transformation T(p,resp), mapping the reference domain to the deformed domain

Parameters:

	p	The point on the reference domain
	resp	To contain the point on the real domain

Returns:

Definition at line 117 of file mappingorthomesh.h.

  {
    assert(p.size() == 3);
    assert(resp.size() == 3);
    resp(0)=_X0[0] + _dx*p(0);
    resp(1)=_X0[1] + _dy*p(1);
    resp(2)=_X0[2] + _dz*p(2);

  }

virtual void MappingOrthoMesh::T_grad	(	const VecDouble &	xi,
		Matrix &	gradT
	)			[inline, virtual]

We generally need the T_Grad when we are computing the jacobian on the faces, in the orthomesh case the gradient is always constant

Parameters:

	xi	The point on the reference domain
	TGrad	To contain the gradient of T on that point

Returns:

Definition at line 103 of file mappingorthomesh.h.

  {
    assert(xi.size() == 3);
    gradT=_GradT;
  }

---

Member Data Documentation

double MappingOrthoMesh::_dx [protected]

Definition at line 18 of file mappingorthomesh.h.

double MappingOrthoMesh::_dy [protected]

Definition at line 18 of file mappingorthomesh.h.

double MappingOrthoMesh::_dz [protected]

Definition at line 18 of file mappingorthomesh.h.

Matrix MappingOrthoMesh::_GradT [protected]

Definition at line 17 of file mappingorthomesh.h.

Matrix MappingOrthoMesh::_invGradT [protected]

Definition at line 17 of file mappingorthomesh.h.

double MappingOrthoMesh::_j [protected]

Definition at line 16 of file mappingorthomesh.h.

const OrthoMesh* MappingOrthoMesh::_pMesh [protected]

Definition at line 19 of file mappingorthomesh.h.

Point3D MappingOrthoMesh::_X0 [protected]

Definition at line 15 of file mappingorthomesh.h.

---

The documentation for this class was generated from the following file:

• mappingorthomesh.h