ConservativeMethod Class Reference

#include <conservativemethod.h>

Inheritance diagram for ConservativeMethod:

[legend]

Collaboration diagram for ConservativeMethod:

[legend]

List of all members.

Public Member Functions
void	getValuesOfTheFaceCells (OrthoMesh &mesh, const VecDouble &fBCValues, const VecDouble &cValues, Index face_index, Index CellNeg, Index CellPos, double &SwNeg, double &SwPos)
void	getValuesOfTheFaceCells (OrthoMesh &mesh, const VecDouble &fBCValues, const VecDouble &cValues, OrthoMesh::Cash_Face_It &face, double &SwNeg, double &SwPos)
void	getValuesOfTheFaceCells (OrthoMesh &mesh, const VecDouble &fBCValues, const VecDouble &cValues, OrthoMesh::Face_It &face, double &SwNeg, double &SwPos)
double	calculateTimeStep (OrthoMesh &mesh, double tEnd, double MaxCFL, const VecDouble &vPorosity, FaceFluxFunction &flux)
	ConservativeMethod ()
virtual	~ConservativeMethod ()
Protected Member Functions
void	buildDerivatives (OrthoMesh &mesh, const VecDouble &cV, Matrix &MG)
void	getCellDerivatives (const VecDouble &sol, const OrthoMesh::Cell_It &cell, double *s0, double *s1, double *s2)

---

Detailed Description

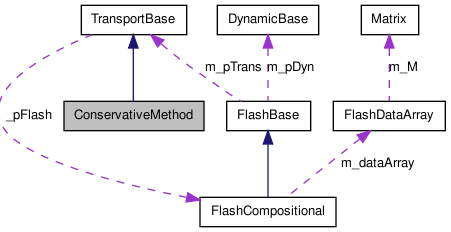
The base class of all conservative scalar methods. See Leveque for a definition of conservative method. This class implement some methods common to all classes that solve the hyperbolic equation doing expression Sw(n+1) = Sw(n) + div(NumericFlux) where the div are aproximated doing a computation along the cells of the grid.

This class assumes that we have an orthonormal uniform grid since it holds a reference for an OrtoMesh object.

Definition at line 17 of file conservativemethod.h.

---

Constructor & Destructor Documentation

ConservativeMethod::ConservativeMethod

(

)

[inline]

Definition at line 32 of file conservativemethod.h.

{}

virtual ConservativeMethod::~ConservativeMethod

(

)

[inline, virtual]

Definition at line 33 of file conservativemethod.h.

{}

---

Member Function Documentation

void ConservativeMethod::buildDerivatives	(	OrthoMesh &	mesh,
		const VecDouble &	cV,
		Matrix &	MG
	)			[protected]

Store the min mod derivatives of the three directions of each cell in a matrix with dimensions [NUM_CELLS][3]

Parameters:

	cV	Vector with solution in each cell
	MG	The matrix containing the derivatives.

Returns:

Definition at line 199 of file conservativemethod.cpp.

{
 
  assert(MG.m() == mesh.numCells());
  assert(MG.n() == 3);
  assert(cV.size() == mesh.numCells());

  OrthoMesh::Cell_It cell = mesh.begin_cell();
  OrthoMesh::Cell_It endc = mesh.end_cell();
  double s0,s1,s2;
  for (;cell != endc; cell++)
  {
    getCellDerivatives(cV,cell,&s0,&s1,&s2);
    MG(cell->index(),0)=s0;
    MG(cell->index(),1)=s1;
    MG(cell->index(),2)=s2;
  } 
}

double ConservativeMethod::calculateTimeStep	(	OrthoMesh &	mesh,
		double	tEnd,
		double	MaxCFL,
		const VecDouble &	vPorosity,
		FaceFluxFunction &	flux
	)

This function calculates the right time step to iterate throw t=0 to t=tEnd such that the Maximum CFL does not exceed the value of the parameter MaxCFL. For orthoMesh this is a easy calculation. The CFL condition for 1D states that Max(VelX) * dt < CFL *dX where dt,dx are the discretization in time and space and Max(VelX) is the maximum velocity of a characteristic line (in other way, the slope of the characteristic line in the time x space plane). For 3D orthogonal meshes in 3D this can be easy extended changing Max(VelX) to Max(VelX,VelY,VelZ) where X,Y,Z are the main axes. IN the case of immiscible flows VelX = fMobW*Vdt where fMob is the mobility function and Vdt is the velocity supplied by the dynamic modules. The calculation principles of these method follows for the case of immiscible flow. fMob(Sw)*Vdt *dt < MaxCFL*dX <=> (1) fMob(Sw)*(Vdt/dX) * dt < MaxCFL <=> (2) Max(fMob(Sw))* Max (Vdt/dX) * dt < MaxCFL (3) Substituting dt = tEnd/numSteps where the numSteps is the number of subdivisions in time, we have to find the max possible value of numSteps such that inequation (3) is obeyed.

Parameters:

	tEnd	The end time of the iteration
	MaxCFL	The Max CFL number the method should have at all domain
	dMaxGradMobW	The max derivative of the mobility function.
	fVelocity	The velocity field supplied by the dinamic module.

Returns:

The right time step;

Definition at line 159 of file conservativemethod.cpp.

{
  double dMinPor = NumericMethods::vectorMinValue(vPorosity);
  double dMinTravelTime; //Travel time is the time the solution needs to cross a cell.

  //Get the discretization steps in each dimension
  double dX = mesh.getDX()[0];
  double dY = mesh.getDX()[1];
  double dZ = mesh.getDX()[2];

  //Get the maximum chracteristic velocity in the three components
  double MaxCharVel[3];
  flux.maxGlobalCharVelocity(MaxCharVel);
  dMinTravelTime=0.0;

  //Min time to cross a cell  in the X direction
  if (MaxCharVel[X] != 0.0)
    dMinTravelTime = dX/fabs(MaxCharVel[X]);
  printf("Max Vel %g %g %g\n",MaxCharVel[0],MaxCharVel[1],MaxCharVel[2]);

  //Min time to cross a cell  in the Y direction
  if (MaxCharVel[Y] != 0.0)
    dMinTravelTime = fmin(dY/fabs(MaxCharVel[Y]), dMinTravelTime);

 //Min time to cross a cell  in the Z direction
  if (MaxCharVel[Z] != 0.0)
    dMinTravelTime = fmin(dZ/fabs(MaxCharVel[Z]), dMinTravelTime);

 return tEnd/ceil(tEnd/(dMinPor*dMinTravelTime*MaxCFL));
 
}

void ConservativeMethod::getCellDerivatives	(	const VecDouble &	sol,
		const OrthoMesh::Cell_It &	cell,
		double *	s0,
		double *	s1,
		double *	s2
	)			[protected]

Return the MinMod Derivatives of a Cell

Parameters:

	sol	= Solution
	OrthoMesh	mesh
	s0	Derivative in X
	s1	Derivative in Y
	s2	Derivative in Z

Returns:

Definition at line 228 of file conservativemethod.cpp.

{
  //Derivative for x
  const OrthoMesh &mesh=cell->getMesh();
  Index li,ri;
  double u = sol(cell->index());
  li = cell->neighbor_index(LEFT_CELL);
  ri = cell->neighbor_index(RIGHT_CELL);
  if (li == OrthoMesh::INVALID_INDEX || ri == OrthoMesh::INVALID_INDEX)
     *s0 = 0.0;
  else
    *s0=NumericMethods::minMod(u-sol(li),sol(ri)-u)/mesh.get_dx();
  

  li = cell->neighbor_index(FRONT_CELL);
  ri = cell->neighbor_index(BACK_CELL);
  if (li == OrthoMesh::INVALID_INDEX || ri == OrthoMesh::INVALID_INDEX)
     *s1 = 0.0;
  else
    *s1=NumericMethods::minMod(u-sol(li),sol(ri)-u)/mesh.get_dy();

  li = cell->neighbor_index(BOTTOM_CELL);
  ri = cell->neighbor_index(UP_CELL);
  if (li == OrthoMesh::INVALID_INDEX || ri == OrthoMesh::INVALID_INDEX)
     *s2 = 0.0;
  else
    *s2=NumericMethods::minMod(u-sol(li),sol(ri)-u)/mesh.get_dz();
}

void ConservativeMethod::getValuesOfTheFaceCells	(	OrthoMesh &	mesh,
		const VecDouble &	fBCValues,
		const VecDouble &	cValues,
		OrthoMesh::Face_It &	face,
		double &	SwNeg,
		double &	SwPos
	)

Definition at line 95 of file conservativemethod.cpp.

{
  assert(fBCValues.size() == mesh.numFaces());
  assert(cValues.size() == mesh.numCells());
  unsigned cPos,cNeg;
  face->getAdjCellIndices(cNeg,cPos);

  unsigned Null = OrthoMesh::invalidIndex();
  if (cPos != Null)
  {
    //get the positive value
    SwPos = cValues(cPos);
    //get the negative value if it exist
    if (cNeg != Null)
      SwNeg = cValues(cNeg);
    else
    {

      //if the neg value doesnt exist,
      //try to see if there is boundary condition
      //for the face
      SwNeg = fBCValues(face->index());
      if (SwNeg == INFINITY) //boundary condition is not defined ?
        SwNeg = SwPos; //If not exist boundary condition, use the value of the positive cell
    }
  }
  else
  {
    //The positive value does not exist,
    //So the Negative value must exist. Get it
    SwNeg = cValues(cNeg);

    //Now take the value for SwPos from the boundary
    //condition or make it equal to the value of the negative cell.
    SwPos = fBCValues(face->index());
    if (SwPos == INFINITY) //Is boundary condition not defined ?
      SwPos = SwNeg;
  }
}

void ConservativeMethod::getValuesOfTheFaceCells	(	OrthoMesh &	mesh,
		const VecDouble &	fBCValues,
		const VecDouble &	cValues,
		OrthoMesh::Cash_Face_It &	face,
		double &	SwNeg,
		double &	SwPos
	)

Definition at line 54 of file conservativemethod.cpp.

{
  assert(fBCValues.size() == mesh.numFaces());
  assert(cValues.size() == mesh.numCells());
  unsigned cPos,cNeg;
  face->getAdjCellIndices(cNeg,cPos);

  unsigned Null = OrthoMesh::invalidIndex();
  if (cPos != Null)
  {
    //get the positive value
    SwPos = cValues(cPos);
    //get the negative value if it exist
    if (cNeg != Null)
      SwNeg = cValues(cNeg);
    else
    {

      //if the neg value doesnt exist,
      //try to see if there is boundary condition
      //for the face
      SwNeg = fBCValues(face->index());
      if (SwNeg == INFINITY) //boundary condition is not defined ?
        SwNeg = SwPos; //If not exist boundary condition, use the value of the positive cell
    }
  }
  else
  {
    //The positive value does not exist,
    //So the Negative value must exist. Get it
    SwNeg = cValues(cNeg);

    //Now take the value for SwPos from the boundary
    //condition or make it equal to the value of the negative cell.
    SwPos = fBCValues(face->index());
    if (SwPos == INFINITY) //Is boundary condition not defined ?
      SwPos = SwNeg;
  }
}

void ConservativeMethod::getValuesOfTheFaceCells	(	OrthoMesh &	mesh,
		const VecDouble &	fBCValues,
		const VecDouble &	cValues,
		Index	face_index,
		Index	cNeg,
		Index	cPos,
		double &	SwNeg,
		double &	SwPos
	)

First of all, this is an internal method used to get the values in the left and in the right of a face. This function exist because there is complications to get this values from the cells adjacents to the faces at boundary. In this case the face has just one neighbour cell and the value in the other inexistent cell must be get from the boundary conditions for the face in the case that condition exist. If not exist we make the value of the inexistent cell (ghost cell) identical to the value of the cell inside the mesh.

Parameters:

	face	The face from wich we get the two values of saturation
	SwNeg	To contain the value in the vector cValues for the cell in the negative direction from the face.
	SwPos	To contain the value in the vector cValues for the cell in the positive direction from the face.

Definition at line 14 of file conservativemethod.cpp.

{
  assert(fBCValues.size() == mesh.numFaces());
  assert(cValues.size() == mesh.numCells());

  static unsigned Null = OrthoMesh::invalidIndex();
  if (cNeg != Null)
  {
    //get the negative value
    SwNeg = cValues(cNeg);

    //get the positive value if it exist
    if (cPos != Null)
      SwPos = cValues(cPos);
    else
    {

      //if the pos value doesnt exist,
      //try to see if there is boundary condition
      //for the face
      SwPos = fBCValues(face_index);
      if (SwPos == INFINITY) //boundary condition is not defined ?
        SwPos=SwNeg; //If not exist boundary condition, use the value of the negative cell
    }
  }
  else
  {
    //The negative  value does not exist,
    //So the Positive value must exist. Get it
    SwPos = cValues(cPos);

    //Now take the value for SwNeg from the boundary
    //condition or make it equal to the value of the positive cell.
    SwNeg = fBCValues(face_index);
    if (SwNeg == INFINITY) //Is boundary condition not defined ?
      SwNeg = SwPos;
  }
}

---

The documentation for this class was generated from the following files:

• conservativemethod.h
• conservativemethod.cpp