ConservativeMethodForSystem Class Reference

#include <conservativemethodforsystem.h>

Inheritance diagram for ConservativeMethodForSystem:

[legend]

Collaboration diagram for ConservativeMethodForSystem:

[legend]

List of all members.

Public Member Functions
	ConservativeMethodForSystem ()
virtual	~ConservativeMethodForSystem ()
virtual void	updateFixedPressureBC (Function3D *fDP, FlashCompositional &flash)=0
Protected Member Functions
void	buildDerivatives (OrthoMesh &mesh, const VecDouble &cV, Matrix &MG)
void	getCellDerivatives (const VecDouble &sol, const OrthoMesh::Cell_It &cell, double *s0, double *s1, double *s2)
bool	getValuesOfTheFaceCells (OrthoMesh &mesh, VecIncBC &vbc, const ArrayOfVecDouble &vcValues, Index face_index, Index negCell, Index posCell, VecDoubleRef &vSwNeg, VecDoubleRef &vSwPos)
bool	getValuesOfTheFaceCellsScalar (OrthoMesh &mesh, VecIncBC &vbc, const VecDouble &cValues, Index face_index, Index negCell, Index posCell, double *dNeg, double *dPos)
double	calculateTimeStep (OrthoMesh &mesh, double tEnd, double MaxCFL, const VecDouble &vPorosity, FaceFluxFunction &flux)

---

Detailed Description

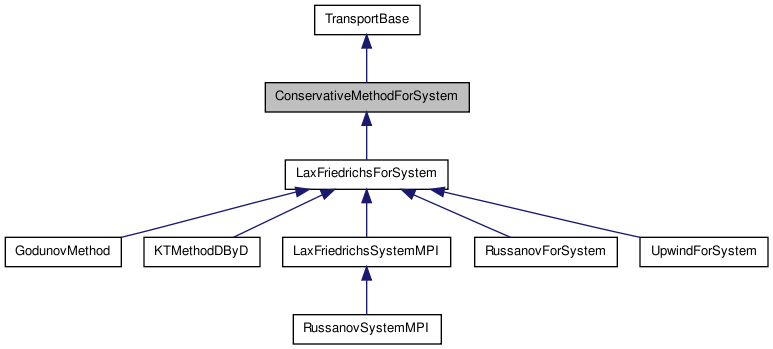
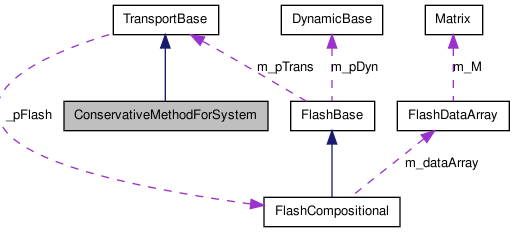
The base class of all conservative methods for hyperbolic systems. See Leveque for a definition of conservative method. This class implement some methods common to all classes that solve the system of hyperbolic equations of the form Sw(n+1) = Sw(n) + div(NumericFlux) where the div are aproximated doing a computation along the cells of the grid.

This class assumes that we have an orthonormal uniform grid since its methods usually uses reference for an OrtoMesh object.

Definition at line 22 of file conservativemethodforsystem.h.

---

Constructor & Destructor Documentation

ConservativeMethodForSystem::ConservativeMethodForSystem

(

)

[inline]

Definition at line 38 of file conservativemethodforsystem.h.

{}

virtual ConservativeMethodForSystem::~ConservativeMethodForSystem

(

)

[inline, virtual]

Definition at line 39 of file conservativemethodforsystem.h.

{}

---

Member Function Documentation

void ConservativeMethodForSystem::buildDerivatives	(	OrthoMesh &	mesh,
		const VecDouble &	cV,
		Matrix &	MG
	)			[protected]

Store the min mod derivatives of the three directions of each cell in a matrix with dimensions [NUM_CELLS][3]

Parameters:

	cV	Vector with solution in each cell
	MG	The matrix containing the derivatives.

Returns:

Definition at line 241 of file conservativemethodforsystem.cpp.

{
 
  assert(MG.m() == mesh.numCells());
  assert(MG.n() == 3);
  assert(cV.size() == mesh.numCells());

  OrthoMesh::Cell_It cell = mesh.begin_cell();
  OrthoMesh::Cell_It endc = mesh.end_cell();
  double s0,s1,s2;
  for (;cell != endc; cell++)
  {
    getCellDerivatives(cV,cell,&s0,&s1,&s2);
    MG(cell->index(),0)=s0;
    MG(cell->index(),1)=s1;
    MG(cell->index(),2)=s2;
  } 
}

double ConservativeMethodForSystem::calculateTimeStep	(	OrthoMesh &	mesh,
		double	tEnd,
		double	MaxCFL,
		const VecDouble &	vPorosity,
		FaceFluxFunction &	flux
	)			[protected]

First of all, this is an internal method used to get the values in the left and in the right of a face. This function exist because there is complications to get this values from the cells adjacents to the faces at boundary. In this case the face has just one neighbour cell and the value in the other inexistent cell must be get from the boundary conditions for the face in the case that condition exist. If not exist we make the value of the inexistent cell (ghost cell) identical to the value of the cell inside the mesh.

Parameters:

	face	The face from wich we get the two values of saturation
	SwNeg	Vector to contain the value for the cell in the negative direction from the face for each component of the system.
	SwPos	Vector to contain the value for the cell in the positive direction from the face for each component of the system.

void ConservativeMethodForSystem::getValuesOfTheFaceCells(OrthoMesh &mesh, const VecIncBC &vbc, const ArrayOfVectors& vcValues, Index face_index, Index negCell, Index posCell, VecDouble &vSwNeg,VecDouble &vSwPos) { check vector dimensions const unsigned n_components = vSwPos.size(); assert(vfBCValues.size() == n_components); assert(vSwNeg.size() == n_components); assert(vcValues.size() == n_components);

for each variable (component) of the system for (unsigned cmp=0;cmp<n_components;cmp++) { getValuesOfTheFaceCells(mesh,vfBCValues[cmp],vcValues[cmp],face_index,negCell,posCell,vSwNeg(cmp),vSwPos(cmp)); } } Calculate the time step to advance the transport method. The time step is returned as a multiple of tEnd If tEnd == INFINITY, than the procedure returns an exact mathc for the time step

Parameters:

	mesh
	tEnd	Amount of time the transport should iterate
	MaxCFL
	vPorosity
	flux

Returns:

Definition at line 48 of file conservativemethodforsystem.cpp.

{
  double dMinPor = NumericMethods::vectorMinValue(vPorosity);
  double dInvMinTravelTime; //Travel time is the time the solution needs to cross a cell.

  //Get the discretization steps in each dimension
  double dX = mesh.getDX()[0];
  double dY = mesh.getDX()[1];
  double dZ = mesh.getDX()[2];

  //Get the maximum chracteristic velocity in the three components
  double MaxCharVel[3];
  flux.maxGlobalCharVelocity(MaxCharVel);

  //To avoid division by zero we calculate the inverse
  //of the min travel time and then we invert the number.

  //Min time to cross a cell  in the X direction
  dInvMinTravelTime = fabs(MaxCharVel[X])/dX;

  //Min time to cross a cell  in the Y direction
  dInvMinTravelTime = fmax(fabs(MaxCharVel[Y])/dY, dInvMinTravelTime);

 //Min time to cross a cell  in the Z direction
 dInvMinTravelTime = fmax(fabs(MaxCharVel[Z])/dZ, dInvMinTravelTime);

 
 if (dInvMinTravelTime == 0)
   return tEnd;

 //double dTravelTime = 1.0/dInvMinTravelTime;
 
 if (tEnd == INFINITY)
   return dMinPor*MaxCFL/dInvMinTravelTime; 
 else
   return tEnd/ceil(tEnd*dInvMinTravelTime/(dMinPor*MaxCFL));

}

void ConservativeMethodForSystem::getCellDerivatives	(	const VecDouble &	sol,
		const OrthoMesh::Cell_It &	cell,
		double *	s0,
		double *	s1,
		double *	s2
	)			[protected]

Return the MinMod Derivatives of a Cell

Parameters:

	sol	= Solution
	OrthoMesh	mesh
	s0	Derivative in X
	s1	Derivative in Y
	s2	Derivative in Z

Returns:

Definition at line 270 of file conservativemethodforsystem.cpp.

{
  //Derivative for x
  const OrthoMesh &mesh=cell->getMesh();
  Index li,ri;
  double u = sol(cell->index());
  li = cell->neighbor_index(LEFT_CELL);
  ri = cell->neighbor_index(RIGHT_CELL);
  if (li == OrthoMesh::INVALID_INDEX || ri == OrthoMesh::INVALID_INDEX)
     *s0 = 0.0;
  else
    *s0=NumericMethods::minMod(u-sol(li),sol(ri)-u)/mesh.get_dx();
  

  li = cell->neighbor_index(FRONT_CELL);
  ri = cell->neighbor_index(BACK_CELL);
  if (li == OrthoMesh::INVALID_INDEX || ri == OrthoMesh::INVALID_INDEX)
     *s1 = 0.0;
  else
    *s1=NumericMethods::minMod(u-sol(li),sol(ri)-u)/mesh.get_dy();

  li = cell->neighbor_index(BOTTOM_CELL);
  ri = cell->neighbor_index(UP_CELL);
  if (li == OrthoMesh::INVALID_INDEX || ri == OrthoMesh::INVALID_INDEX)
     *s2 = 0.0;
  else
    *s2=NumericMethods::minMod(u-sol(li),sol(ri)-u)/mesh.get_dz();
}

bool ConservativeMethodForSystem::getValuesOfTheFaceCells	(	OrthoMesh &	mesh,
		VecIncBC &	vbc,
		const ArrayOfVecDouble &	cvcValues,
		Index	face_index,
		Index	negCell,
		Index	posCell,
		VecDoubleRef &	vSwNeg,
		VecDoubleRef &	vSwPos
	)			[protected]

Usefull method to get the Solution of the cells located between a face. This method consider the boundary condition information stored in the parameter vbc to get always valid values, even for the faces in the boundary. For a face inside the domain it just return the values based on the solution passed in the cvcValues parameter.

If the face is at boundary, and there is no boundary condition prescribed the value of the cell out of the mesh is equal to the value of the cell inside the mesh. This is called a mirror condition

If there is a boundary condition, this value is returned.

Parameters:

	mesh	The OrthoMesh
	vbc	Vector containing the bc info
	cvcValues	ArrayOfVectors containing the solution for each component of the solution (Remember that we are solving a system of equations)
	face	The index of the face
	negCell	The cell on the negative side of the face, -1 if it does not exist (Remember: face can be on the boundary)
	posCell	The cell on the positive side of the face, -1 if it does not exist (Remember: face can be on the boundary)
	vSwNeg	To contain the solution of the negative cell
	vSwPos	To contain the solution of the positive cell

Returns:

true if there was a boundary condition for that face, false if there are none. In the case that the face is at boundary and there is no boundary condition, the mirror bc is used.

Definition at line 122 of file conservativemethodforsystem.cpp.

{
  ArrayOfVecDouble &vcValues=const_cast<ArrayOfVecDouble&>(cvcValues);
  assert(vSwNeg.size() == vbc.bc_dim());
  assert(vSwPos.size() == vbc.bc_dim());
  if (posCell != OrthoMesh::invalidIndex())
  {
    //get the positive value
    vcValues.getVecValues(posCell,&vSwPos);

    //get the negative value if it exist
    if (negCell != OrthoMesh::invalidIndex())
    {
      vcValues.getVecValues(negCell,&vSwNeg);
      return false;
    }
    else
    {

      //if the neg value doesnt exist,
      //try to see if there is boundary condition
      //for the face
      if (vbc.get_ref_bc(face_index,vSwNeg))
      {
        return true;
      }
      else
      {
        //If not use mirror condition
        vcValues.getVecValues(posCell,&vSwNeg);
        return false;
      }
   }
  }
  else
  {
    //The positive value does not exist,
    //So the Negative value must exist. Get it
    vcValues.getVecValues(negCell,&vSwNeg);

    //Now take the value for SwPos from the boundary
    //condition or make it equal to the value of the negative cell.
    if (vbc.get_ref_bc(face_index,vSwPos)) //Ok BC exists
    {
      return true;
    }
    else
    {
      //If not use mirror condition
      vcValues.getVecValues(negCell,&vSwPos);
      return false;
    }
  }
  assert(0);
  return false;
}

bool ConservativeMethodForSystem::getValuesOfTheFaceCellsScalar	(	OrthoMesh &	mesh,
		VecIncBC &	vbc,
		const VecDouble &	cValues,
		Index	face_index,
		Index	negCell,
		Index	posCell,
		double *	dNeg,
		double *	dPos
	)			[protected]

Definition at line 179 of file conservativemethodforsystem.cpp.

{
  bool result=false;
  static VecDouble vSw(1);
  assert(vbc.bc_dim()==1);
  if (posCell != OrthoMesh::invalidIndex())
  {
    //get the positive value
    *dPos = cValues(posCell);

    //get the negative value if it exist
    if (negCell != OrthoMesh::invalidIndex())
      *dNeg=cValues(negCell);
    else
    {

      //if the neg value doesnt exist,
      //try to see if there is boundary condition
      //for the face
      if (vbc.copy_bc(face_index,vSw))
      {
        result=true;
        *dNeg=vSw(0);
      }
      else
      {
        //If not use mirror condition
        *dNeg=*dPos;
      }
   }
  }
  else
  {
    //The positive value does not exist,
    //So the Negative value must exist. Get it
    *dNeg = cValues(negCell);

    //Now take the value for SwPos from the boundary
    //condition or make it equal to the value of the negative cell.
    if (vbc.copy_bc(face_index,vSw))
    {
      *dPos=vSw(0);
      result=true;
    }
    else
    {
      *dPos=*dNeg; 
    }
  }
  return result;
  
}

virtual void ConservativeMethodForSystem::updateFixedPressureBC	(	Function3D *	fDP,
		FlashCompositional &	flash
	)			[pure virtual]

Implemented in LaxFriedrichsForSystem.

---

The documentation for this class was generated from the following files:

• conservativemethodforsystem.h
• conservativemethodforsystem.cpp